C++算法练习 | Godown

算法练习（C++代码）

快速幂算法

题目：输入一个整数 n ，求 n^n 的个位数是多少。

快速幂算法：指数为偶数，则底数平方，指数除二；指数为奇数，则指数减一再把结果乘底数，底数平方，指数除二。指数看作二进制，除二可以看作位运算。

#include <iostream>

using namespace std;
int main(){
	int n;
	cin>>n;
	int power=n;
	int base=n;
	int result = 1;
	while(power>0){
		if(power%2==1){
			result *= base;
			power /= 2;
			base *= base;//指数为奇数，先乘底数。除二小数部分舍去。底数平方 
		}
		else{
			power /= 2;
			base *= base;//指数为偶数，除二，底数平方 
		}
	}
	cout<<result<<endl; 
	cout<<result%10;//mod 10即个位数
}

斐波那契

输入一个整数 n ，求斐波那契数列的第 n 项。第一项是1，第二项是1。要求必须递归！

#include <iostream>

using namespace std;

int f(int n){
    if(n==1||n==2){
        return 1;
    }
    else return f(n-2)+f(n-1);
}

int main(){
    int n;
    cin >> n;
    cout<<f(n);
}

成绩排名

对 n 个同学的考试成绩从大到小排名，成绩相同的算同一名。求排名为 m 的成绩。若无排名为m的成绩，输出最后一名的成绩。

输入格式

一共三行

第一行：一个整数 n，表示同学的个数。

第二行：n 个整数，表示 n 个同学的成绩。

第三行：一个整数 m，表示排名。

输出格式

一个整数，表示排名为 m 的成绩。

输入样例

6
100 100 99 98 97

输出样例

#include <iostream>

using namespace std;
int main(){
	int n,m;
	cout<<"输入同学个数："<<endl;
	cin>>n;
	int score[n];
	cout<<"输入同学的成绩："<<endl;
	for (int i=0;i<n;i++){
		cin>>score[i];
	}
	//cout<<"1";
	for (int i=0;i<n;i++){
		for(int j=n-i-1;j>0;j--){
			if(score[j]>score[j-1]){
				int temp = score[j];
				score[j] = score[j-1];
				score[j-1] = temp;
			}
		}//冒泡排序
	}
	int i=0,j;
	for(j=1;j<n;j++){
		if(score[j]!=score[i]){
			score[++i]=score[j];
		}
	}//双指针去重
	cout<<"输入要查询的排名："<<endl;
	cin>>m;
	if(m>i+1){
		cout<<score[i]<<endl; 
	}
	else{
		cout<<score[m-1];
	}
}

括号匹配

给定三种括号{ }，[ ], ( )，和若干小写字母的字符串，请问改字符串的括号是否匹配（可以嵌套）?

输入输出

输入格式：字符串s。输出格式：若匹配，输出yes，否则输出no。

输入样例

1	{[a(v)d]q}

输出样例

yes

#include <iostream>
#include <stack>

using namespace std;
int main(){
	stack <int> s;
	string strs;
	cin>>strs;
	int m = strs.length();
	for (int i=0;i<m;i++){
		if(strs[i]=='('||strs[i]=='{'||strs[i]=='['){
			s.push(strs[i]);
		}
		if(strs[i]==')'){
			if(!s.empty()&&s.top()=='(') s.pop();
			else{
				cout<<"不匹配"; 
				return 0;
			}
		}
		else if(strs[i]=='}'){
			if(!s.empty()&&s.top()=='{') s.pop();
			else{
				cout<<"不匹配"; 
				return 0;
			}
		}
		else if(strs[i]==']'){
			if(!s.empty()&&s.top()=='[](https://typora-202017030217.oss-cn-beijing.aliyuncs.com/typora/image-20240302154623876.png)

```cpp
//判断回文串

#include <iostream>
#include <string>

using namespace std;

bool isCircel(string &str){
	int m = str.length();
	for(int i=0;i<m/2;i++){//中点结束
		if(str[i]!=str[m-i-1]) return 0;
	}
	return 1;
}
int main(){
	string str;
	getline(cin,str);
	if(isCircel(str)) cout<<"yes";
	else cout<<"No";
	return 0;
}

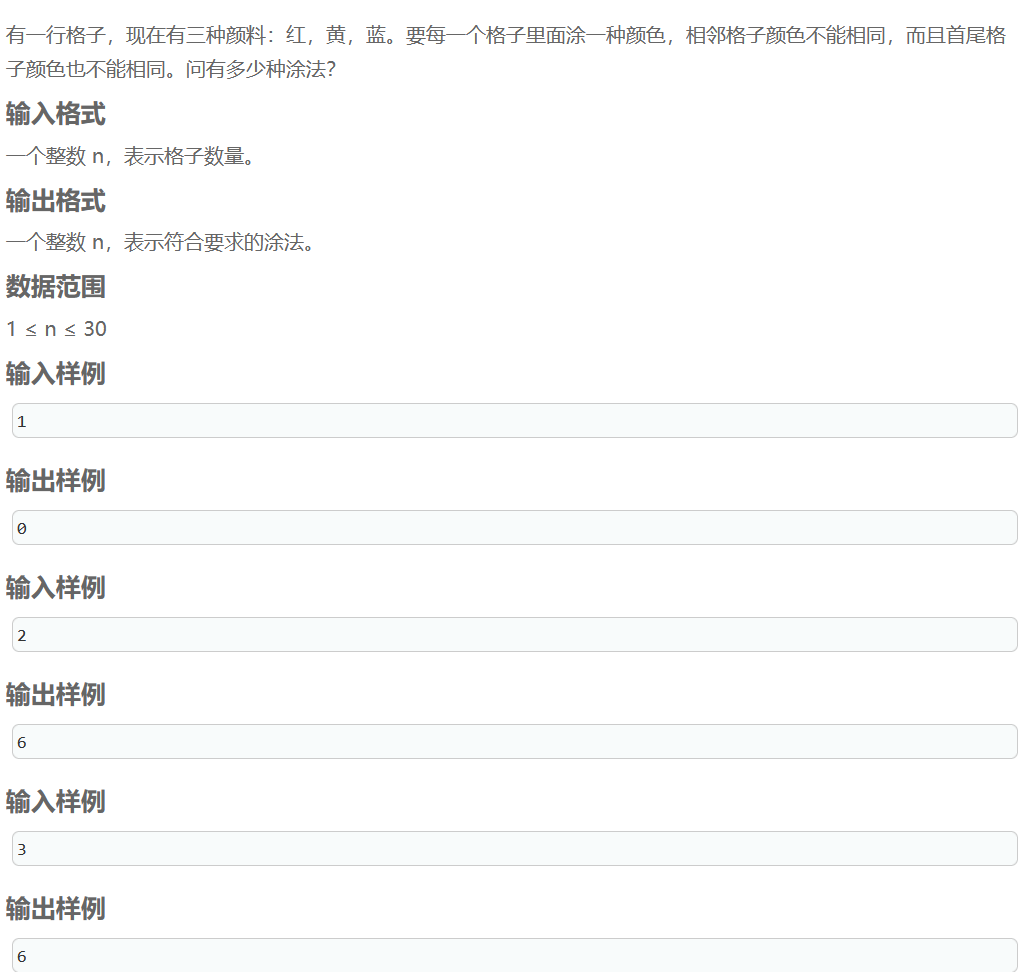
格子涂色

这道题关键在n个格子，n-1格子里什么颜色。

假设n-1格子里和第一个格子颜色相同，则第n个格子可以有两种选择，且f(n-1)=f(n-2)
假设n-1格子里和第一个格子颜色不同，则第n个格子只有一种选择

即第一种情况f(n)=2*f(n-2)，第二种情况f(n)=f(n-1)

递推公式：f(n) = 2*f(n-2) + f(n-1)

且由于n=3时，第三格必不能和前两格颜色相同，所以f(3)=f(2)=6

//格子涂色

#include <iostream>

using namespace std;

int f(int n){
	if(n==3||n==2) return 6;
	if(n==1) return 0;
	return 2*f(n-2) + f(n-1);
}

int main(){
	int n;
	cin >>n;
	cout<<f(n);
	return 0;
}

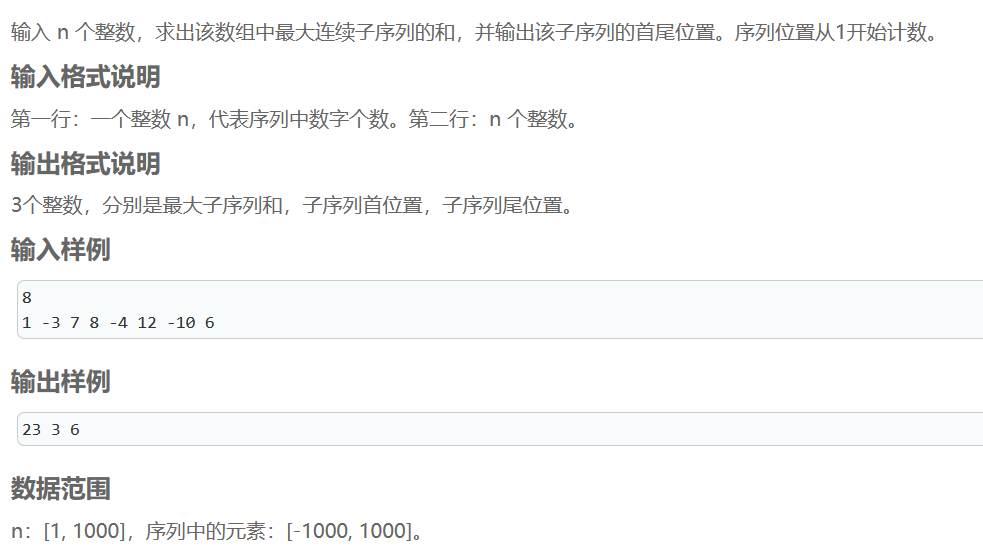
递增最大子序列和

最大的困难，读题：比如1 3 7 2 10的序列，要求找出一个递增子序列，也就是1 3 7满足，1 3 7 2不满足。

//递增子序列最大和

#include <iostream>
#include <vector>

using namespace std;
int f(vector<int> &m){
	int maxsum=0;int n=m.size();
	int temp=m[0];
	for(int i=1;i<n;i++){
		if(m[i]>m[i-1]){//后面一个比前面的大，即递增，加到当前最大和
			temp += m[i];
			if(temp > maxsum){//当前最大和>最大子序列和
				maxsum = temp;
			}
		}
		else{
			temp = m[i];
		}
	}
	return maxsum;
}

int main(){
	int n;
	cin >> n;
	vector<int> m(n);
	for(int i=0;i<n;i++){
		cin>>m[i];
	}
	cout<<f(m);
	return 0;
	
}

最大子序列和

分为两种情况：比如1 -3 7 8 -4 12 -10 6

假如到了i位置，判断这个位置要不要也加入子序列，先判断前面的子序列和是否大于0，比如1 -3相加为-2，则从7开始一定比加上前面的序列和更大。如果前面的子序列大于0，如 7 8 -4，则使用前面的子序列。
如果序列全负，如 -3 -2 -1 -4 -5 -6 -7 -8，则应该子序列只包含-1项。初始化最大子序列和为首项即可，如果初始化为0无法判断上述情况

//最大子序列的和
//从左到右开始加，如果前面所加之和比本身还小，不如更新子序列从本身开始。辅助变量：当前子序列首位址，当前最大子序列和，实际最大子序列和，，实际子序列头，实际子序列尾。 

#include <iostream>
#include <vector>
#define min -31457

using namespace std;

int f(vector<int> &m){
	int n=m.size();
	int front=0,rear=0,tempsum=0,sum=m[0],tempfront=0;//初始化子序列最大和为首项 
	for(int i=0;i<n;i++){
		if(tempsum>0){//前面子序列和大于0，继续使用 
			tempsum += m[i];
			if(tempsum > sum){//加上该位置当前子序列和大于最大子序列和 
				front = tempfront;
				sum = tempsum;
				rear = i;
			}
		}
		else{//前面子序列和小于0 
			tempfront = i;//暂存序列首 
			tempsum = m[i];
		}
		if(tempsum > sum){
			rear = i;
			front = i;
			sum = tempsum;
		}//全负情况，如-3 -2 -1 -4 -5 -6 -7 -8  
	}
	cout<<front+1<<" "<<rear+1<<" "<<sum;
}

int main(){
	int n;
	cin>>n;
	vector<int> m(n);
	for(int i=0;i<n;i++){
		cin>>m[i];
	}
	f(m);
	return 0;
}

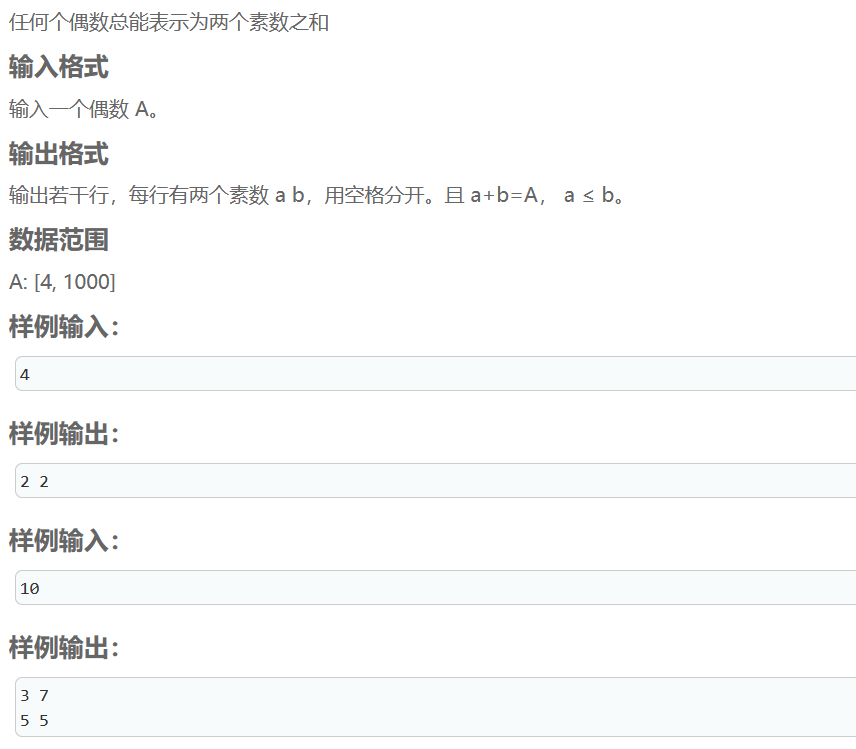
偶数分解

根据数论：如果一个数a不能被从2到sqrt(a)整除，则a为素数

//偶数分解

# include <iostream>
# include <math.h>

using namespace std;

bool isPrime(int n){
	for(int i=2;i<=sqrt(n);i++){
		if(n%i==0){
			return false;
		}
	}
	return true;
}

bool divise(int n){
	bool flag=false; 
	for(int i=2;i<(n/2+1);i++){
		int j=n-i;
		if(isPrime(i)&&isPrime(j)) {
		cout<<i<<" "<<j<<endl;
		flag = true;
		}
	}
	
	return flag;
}

int main(){
	int n;
	cin>>n;
	if(!divise(n)) cout<<"不可分解";
	return 0;
}

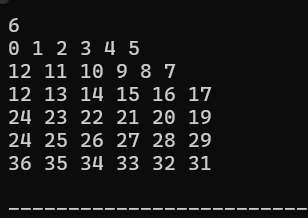
蛇形矩阵

看到这你都还不能自己写我只能送你四个大字，别看了

奇数行正序，偶数行逆序

#include <iostream>

using namespace std;

int main(){
	int n;
	cin>>n;
	for(int i=0;i<n;i++){//i为行 
		for(int j=0;j<n;j++){// 
			if(i%2){//偶数行 
			cout<<n*(i+1)-j<<" ";
			}
			else cout<<n*i+j<<" ";
		}
		cout<<endl;
	}
}

计算第几天

第二个样例输出是错的，应该是159

输入日期yyyy mm dd，输出是本年第几天。

本题主要知识点：年份满足以下条件之一为闰年，2月有29天：

年份能被4整除，不能被100整除

年份能被400整除

//计算第几天

#include <iostream>

using namespace std;

bool isDouYear(int n){
	if((n%4==0&&n%100!=0)||(n%400==0)) return true;
	else return false;
}

int whatday(int year,int month,int day){
	int m[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
	int sumday = 0;
	if(isDouYear(year)) m[2] = 29;
	for(int i=0;i<month;i++){
		sumday += m[i];
	}
	return sumday+day;
}

int main(){
	int year,month,day;
	cin>>year>>month>>day;
	cout<< whatday(year,month,day);
	return 0;
}

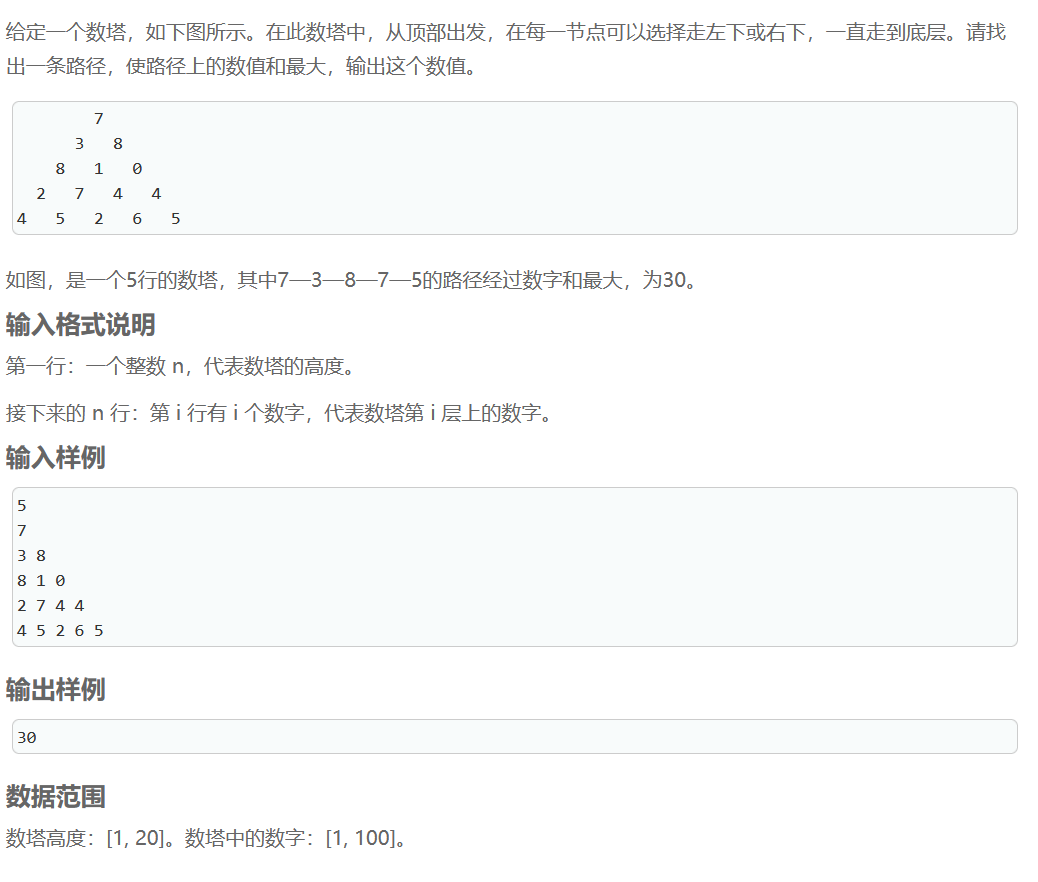
数塔路径

如果不懂可以先看下面letcode三道路径题

数塔中(i,j)来自于(i-1,j-1),(i-1,j)中的最大值，定长数组方便，这里用动态数组

中间排了一个很久的错，push_back是压入向量，但是事先声明了向量会保存，什么意思呢？
1
2
3
4
5
6
7
8
vector<vector<int>> dp(n);//错误来源
	for(int i=0;i<n;i++){
		vector<int> dprow(i+1);
		for(int j=0;j<=i;j++){
			dprow[j]=0;
		}
		dp.push_back(dprow);
	}//定义dp数组 
声明dp数组时放入n个向量，然后dp.push_back的向量是在n个向量之后。应该直接vector<vector<int>> dp;

//三角形最小路径和 
//push_back向vector里压入向量 ，每行第一个只能来自上一行第一个，每行最后一个只能来自上一行最后一个。 
#include <iostream>
#include <vector>
#include <math.h>

using namespace std;

int maxpath(vector<vector<int>> &m){
	int n = m.size();
	vector<vector<int>> dp;
	for(int i=0;i<n;i++){
		vector<int> dprow(i+1);
		for(int j=0;j<=i;j++){
			dprow[j]=0;
		}
		dp.push_back(dprow);
	}//定义dp数组 
	dp[0][0]=m[0][0];
	for(int i=1;i<n;i++){
		for(int j=0;j<=i;j++){
			if(j==0) dp[i][0]=m[i][0]+dp[i-1][0];//数塔最左边只来自上面的最左边
			else if(j==i) dp[i][j]=m[i][j]+dp[i-1][j-1];//同理，最右边来自上面最右边
			else{
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+m[i][j];//(i,j)来自于(i-1,j-1),(i-1,j)中的最大值
			}
			//cout<<dp[i][j]<<" ";
		}
	}
	int maxest=dp[n-1][0];
	for(int i=0;i<n;i++){
		if(dp[n-1][i]>maxest){
			maxest = dp[n-1][i];
		}
	}
	return maxest;
}

int main(){
	int n;//行数
	cin>>n;
	vector<vector<int>> m; 
	for(int i=0;i<n;i++){
		vector<int> row(i+1);//每行i+1个元素 
		for(int j=0;j<=i;j++){
			cin>>row[j];
		}
		m.push_back(row);//向量压栈
	}
	cout<<maxpath(m);
	return 0; 
}

字符统计

别看代码少，很多知识盲区

首先cin不能读取换行符，如果非要使用cin，要用char a;while(cin>>noskipws>>a;&&a!='.');，不推荐，考试也记不起来

getline(cin,str,’.’);以.为分隔符读取字符，前面的空格和换行符也都要读取，默认getline(cin,str)会读空格

getchar()读一个字符。

易错点：字符比较时，’\n’和’.’必须用单引号，双引号会字符串末尾+’\0’，字符和字符串比较会转为整型比较并报错

//字符统计

#include <iostream>
#include <string>

using namespace std;

int main(){
	string strs;
	int skipnum=0,atsum=0;
	getline(cin,strs,'.');
	//cout<<strs;
	int n=strs.length();
	for(int i=0;i<n;i++){
		char str=strs[i];
		if(str=='\n') skipnum++;
		else if(str=='a'){
			if(strs[i+1]=='t') atsum++;
		}
	}
	cout<<skipnum<<" "<<atsum;
}

猜数字

折半查找

//猜数字
//折半查找，王道上有 

#include <iostream>

using namespace std;

int halfseek(int n,int x){
	int mid=n/2;
	int seeknum=0;
	int low=0,high=n;
	while(low<=high){
		mid=(low+high)/2;
		seeknum++;
		if(mid==x) return seeknum-1;
		if(x>mid){
			low=mid+1;
		}
		else{
			high=mid-1;
		}
	}
}

int main(){
	int n,x;
	cin>>n>>x;
	cout<<halfseek(n,x);
}

矩形容纳

n/2*m/2

矩阵覆盖

输出格式那打错了，应该是要覆盖需要的正方形个数

n为奇数则n/2+1，n为偶数则n/2。

矩阵覆盖2

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

根据两个矩形的形状可知，当第一次竖着放的时候，一共有多少方法取决于后面边长为2*(n-1)的矩形中小矩形的放法有多少种；当第一次横着放的时候，必须是横着放两个矩形，一共有多少种方法取决于后面边长为2*(n-2)的矩形中小矩形的放法有多少种。所以总共的放法有f(n)=f(n-1)+f(n-2)。

f(1)=1，f(2)=2

斐波那契

高精度乘法

最难的一道，难到你上网搜csdn和知乎搜出来的答案能看到你脑子爆炸。有三个难点：

怎么存储大整数？大整数怎么加法？大整数怎么乘法？

首先，可以用数组存大整数的每一位，用数组下标表示其位高。可以向string输入，然后减去字符'0'即可得到其每一位数字。

大整数怎么乘？

常规乘法是这样的：

如果199×9，199×9，199×1再移位相加，就要用三个vector存储中间结果，麻烦且空间复杂度高

实际上199×9也是9×9,9×9,1×9的移位加，且各位乘个位必定位数在2以内。

A[i]×B[j]+上一轮的进位就是本轮结果。个位数为C[i+j+1]，十位数为C[i+j]+之前的进位。

可能还是不能理解，模拟一下循环，如图：

重点：string A=123456789，A[8]=9，加减乘是从个位开始的，所以应该逆序

结果也是一样，比如9×9=81，8应该存C[0]，1存C[1]。

//高精度乘法 

#include <iostream>
#include <vector>
#include <string>

using namespace std;

vector<int> pricisemultipy(string &A,string &B){
	vector<int> C(A.size()+B.size(),0); 
	for(int i=A.size()-1;i>=0;i--){
		for(int j=B.size()-1;j>=0;j--){
			int sum = (A[i]-'0')*(B[j]-'0');
			int result = sum + C[i+j+1];//加上一轮的进位
			C[i+j+1] = result % 10 ;//个位 
			C[i+j] += result / 10 ;//十位，还要加上之前那个位置上有的数字
		}
	}
	return C;
}


int main(){
	string A,B;
	cin>>A>>B;
	vector<int> C = pricisemultipy(A,B);
	for(int i=0;i<C.size();i++){
		cout<<C[i];
	}
	
}

最后C数组从高到低就是结果。

算法为了理解，去除了不必要的部分，比如去除高位0和输入0判断。

高精度除法大概率不考，考了也没人能写出来。这个算法请务必多写几遍

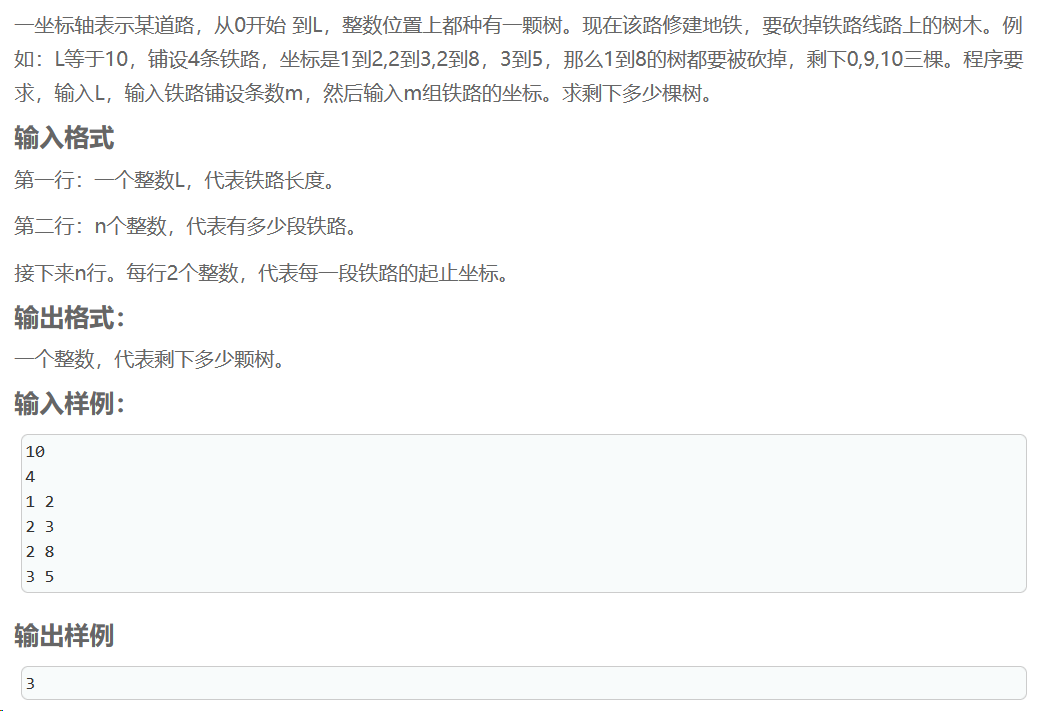
砍树修路

用辅助数组Tree，访问到置为1，最后数0。

易错点：不能int Tree[L+1];，变长数组不会报错但运算会出问题

//砍树修路

#include <iostream>
#include <vector>

using namespace std;

int remain(int L,int n,vector<vector<int>> &a){//0~L的数组，访问到就置为1，最后为0的就是剩余树 
	vector<int> Tree(L+1);//不能int Tree[L+1];，变长数组不会报错但运算会出问题 
	for(int i=0;i<n;i++){
		for(int j=a[i][0];j<=a[i][1];j++){
			Tree[j]=1;
		}
	}
	int sum=0;
	for(int i=0;i<=L;i++){
		if(Tree[i]==0) sum++;
	}
	return sum;
}
int main(){
	int L,n;
	cin>>L>>n;
	vector<vector<int>> a(n,vector<int> (2));
	for(int i=0;i<n;i++){
		cin>>a[i][0]>>a[i][1];
	}
	cout<<remain(L,n,a);
	return 0;
}

letcode&牛客dp+链表

不同路径

先看递归解决：很明显从右下角开始思考，有从上和从左过来两种方式，即等于左和上路径条数之和。1*2，1*3….等很明显只有一条路径，即m or n一个为1，则返回1

#include <iostream>

using namespace std;

int path(int m,int n){
	if(m>1&&n>1){
		return path(m-1,n)+path(m,n-1);
	}else return 1;//1*2或者2*1或者1*6的路径选择都为1个 
}

int main(){
	int m,n;
	cin>>m>>n;
	cout<<path(m,n);
}

很遗憾，递归不满足时间复杂度。

非递归解决：定义一个dp数组，记录每个格子的路径条数，即除一行一列外，每个格子的路径条数都等于上+左

#include <iostream>

using namespace std;

int path(int m,int n){
    int dp[m][n];
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
        	if(j>0&&i>0){
        		dp[i][j]=dp[i-1][j]+dp[i][j-1];
    		}
            else{
                dp[i][j]=1;
            }
        }
    }
    return dp[m-1][n-1];
}

int main(){
	int m,n;
	cin>>m>>n;
	cout<<path(m,n);
}

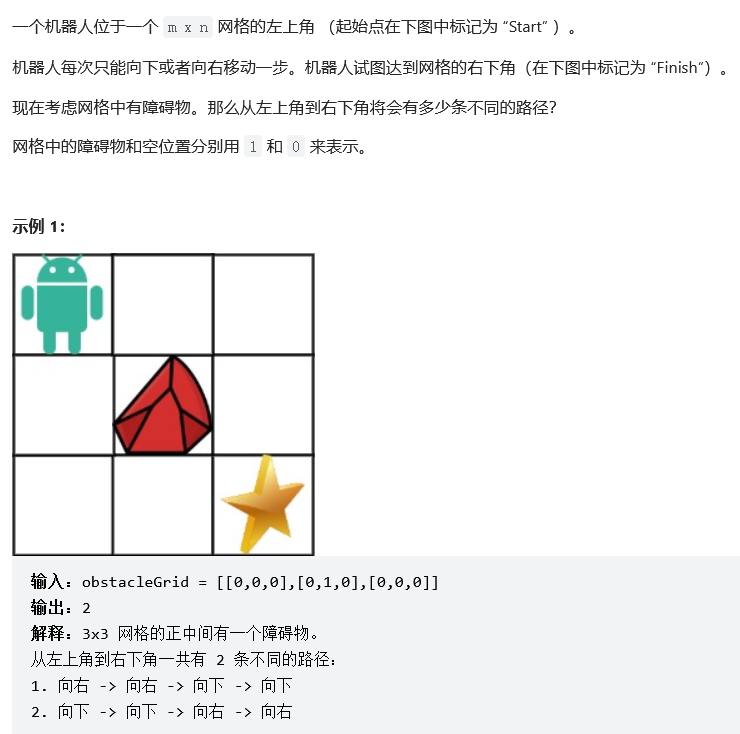
障碍物版不同路径

首先，怎么输入和传参二维数组？

不能直接向某个变量cin二维数组，只能先输入行和列，然后再逐个输入，传参就用vector，因为C++传参定长，不能使用int[][] matrix，而是int matrix[][3]这种，不如使用vector方便

其次，障碍物点到达它的路径条数为0，其余按照上个题目进行计算即可

不能直接把数组传给vector，需要先进行类型转换：

int arr[rows][cols] = {{0, 0, 0}, {0, 1, 0}, {0, 0, 0}};

    // 将数组转换为 std::vector
    vector<vector<int>> matrix;
    for (int i = 0; i < rows; ++i) {
        matrix.push_back(vector<int>(begin(arr[i]), end(arr[i])));
    }

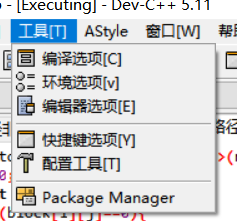
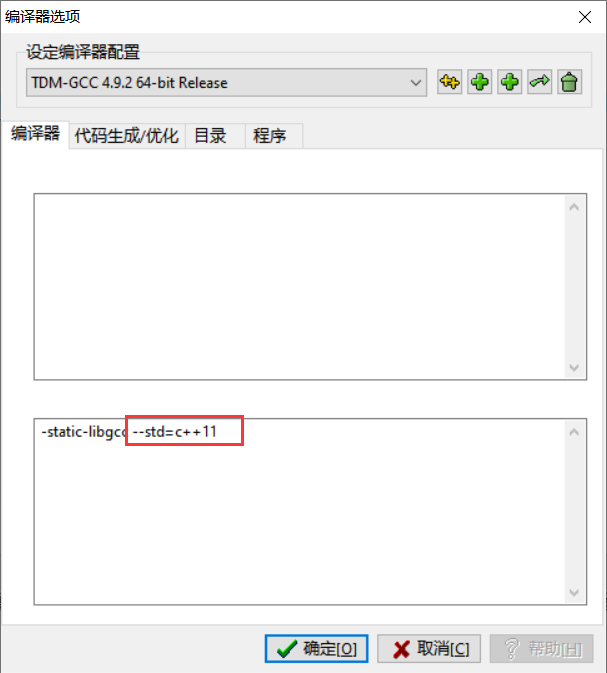
注意：devC++的标准无法读取vector库，需要在编译选项->添加参数”–std=c++11”

#include <iostream>
#include <vector>

using namespace std;
int path(vector<vector<int>>& block){
    int m=block.size(),n=block[0].size();
    vector<vector<int>> dp(m,vector<int>(n));
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(block[i][j]==0){
                if(j>0&&i>0){
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }else{
                    dp[i][j]=1;//第一行或第一列
                }
            }else{
                dp[i][j]=0;//有障碍物
            }
        }
    }
    return dp[m-1][n-1];
}
int main(){
    int rows,cols;
    cout<<"请输入行数和列数："<<endl;
    cin>>rows>>cols;
    vector<vector<int>> block(rows,vector<int>(cols));
    cout<<"请依次输入矩阵："<<endl;
    for(int i=0;i<rows;i++){
        for(int j=0;j<cols;j++){
            cin>>block[i][j];
        }
    }
    cout<<"左上到右下路径条数为："<<path(block);
    return 0;
}

秒了

最小路径和

太经典了，和回复祝顺利一样经典

根据上两道题，不难猜出每个位置的dp最小值为min(上，左)+本块值，第一行则只能左+本块值，第一列则只能上+本块值，秒了

#include <iostream>
#include <vector>

using namespace std;
int min(int n,int m){
    if(n>m) return m;
    else return n;
}
int path(vector<vector<int>>& block){
    int m=block.size(),n=block[0].size();
    vector<vector<int>> dp(m,vector<int>(n));
    dp[0][0]=block[0][0];
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(i>0&&j==0){
                dp[i][j]=dp[i-1][j]+block[i][j];//第一行
            }
			if(j>0&&i==0){
                dp[i][j]=dp[i][j-1]+block[i][j];//第一列
            }
			if(j>0&&i>0){
                dp[i][j]=min(dp[i][j-1],dp[i-1][j])+block[i][j];
            }
        }
    }
    return dp[m-1][n-1];
}
int main(){
    int rows,cols;
    cout<<"请输入行数和列数："<<endl;
    cin>>rows>>cols;
    vector<vector<int>> block(rows,vector<int>(cols));
    cout<<"请依次输入矩阵："<<endl;
    for(int i=0;i<rows;i++){
        for(int j=0;j<cols;j++){
            cin>>block[i][j];
        }
    }
    cout<<"左上到右下最短路径和为："<<path(block);
    return 0;
}

other 机试题

中南大上机压轴

水印是我的CSDN号

测试数据：

3 500
0.6 100
0.8 200
0.7 100
输出 390

首先要对输入的折扣进行排序，优先使用比率低的z进行支付。
然后用lowcost记录目前多少钱是打过折的。T-lowcost就是剩余没打折的。
每次循环用上一个人的折扣额度。若所有人折扣额度相加低于总价，则最后剩的部分就不打折

#include <iostream>
using namespace std;

int paychase(int N,int T,double *z,int* H){
	int lowcost = 0;
	for(int i=0;i<N;i++){
		if(T<=lowcost+z[i]*H[i]){
			T = lowcost + (T-lowcost)*H[i];
			return T;
		}//菜品总价小于折扣
		else{
			lowcost = lowcost + z[i]*H[i];//lowcost为当前折扣限度，比如第二轮中就是0.6*100+0.8*200
			cout<<"lowcost:"<<lowcost<<endl;
			T = T - H[i] + z[i]*H[i];//折扣
			cout<<"T:"<<T<<endl;
		}
	}
	return T;
}

int main(){
	int N,T;
	cout<<"请输入人数和菜品总价："<<endl;
	cin>>N>>T;
	double z[N];
	int H[N];
	cout<<"请输入每个的折扣率和折扣上限："<<endl;
	for(int i=0;i<N;i++){
		//cout<<i<<endl;
		cin>>z[i]>>H[i];
	}
	for (int i=0;i<N;i++){
		for (int j=i;j<N;j++){
			if(z[j]>z[i]){
				double tempz;int tempH;
				tempz=z[j];z[j]=z[i];z[i]=tempz;
				tempH=H[j];H[j]=H[i];H[i]=tempH;
			}
		}//折扣排序
	}
	int cost = paychase(N,T,z,H);
	cout<<"本次用餐总花费："<<cost<<endl;
	return 0;
}

C语言考点

指针数组，数组指针

区分int (*p)[3]和 int *p[3]

指针数组：int *p[3]，实际上是个数组，只是里面元素都存放的指针，指针指向int型变量地址。
数组指针：int (*p)[3]，优先级()>[]>*，实际上是定义的一个指针，指向一个包含三个整数的数组。

int **p

int **p是一个指针的指针。

赋值判断

int *a=&b(√)

int a=&b(×)

int *a; a=&b(√)

记住只有指针才能存地址，整型那些都不能存地址。以及int *a后，*a才是取值，a是指向的地址。

枚举类型中是否可以用小数？枚举类型的值能否修改？

不可以，不能修改

不借助第三个变量，交换两个变量的值

int a = 5, b = 10;

// 使用算术运算符交换两个变量的值
a = a + b;
b = a - b;
a = a - b;

后文会更密码学和C易错点记录

Godown_blog

山水为竭，冬雷震震

算法练习（C++代码）

快速幂算法

斐波那契

成绩排名

括号匹配

格子涂色

递增最大子序列和

最大子序列和

偶数分解

蛇形矩阵

计算第几天

数塔路径

字符统计

猜数字

矩形容纳

矩阵覆盖

矩阵覆盖2

高精度乘法

砍树修路

letcode&牛客dp+链表

不同路径

障碍物版不同路径

最小路径和

other 机试题

中南大上机压轴

C语言考点

指针数组，数组指针

int **p

赋值判断

枚举类型中是否可以用小数？枚举类型的值能否修改？

不借助第三个变量，交换两个变量的值